Временные оценки на информационных графах
Информационный граф отображает порядок следования работ. Тогда очевидно, что момент окончания выполнения любой работы (если началом отсчёта времени является момент начала выполнения работ — начало выполнения алгоритма) не может быть меньше максимальной из длин всех путей, которые заканчиваются вершиной, соответствующей этой работе.
Таким образом, для каждой i = 1 , ... , m работы алгоритма, представленного информационным графом, можно найти ранний срок ?1i окончания её выполнения. Если же выполнение алгоритма ограничено временем T < Tкр, то для каждой работы можно найти и поздний срок ?2i(T) окончания её выполнения. Окончание выполнения i-й работы позже этого срока приводит к тому, что выполнение других работ, следующих за данной, не может быть закончено до истечения времени T. Иначе говоря, поздний срок окончания выполнения данной работы не может превышать разности между значением T и максимальной из длин путей, в первую вершину которых входит дуга, что исходит из вершины, соответствующей данной работе. Без задания значения T (ограничения на длительность вычислительного процесса) определение позднего срока окончания выполнения работы не имеет смысла.
При T = Tкр ранние сроки окончания выполнения работ, составляющих критические пути, совпадают с поздними сроками окончания их выполнения.
Прежде чем рассмотреть алгоритм нахождения ранних и поздних сроков окончания выполнения работ по расширенной матрице следования S*, отметим, что учёт транзитивных связей увеличивает число необходимых действий. Так как граф G не содержит контуров, то матрица следования S может быть преобразована в треугольную. Однако при построении алгоритмов решения задач распараллеливания не представляется удобным преобразовывать матрицу следования. Поэтому будем считать, что в общем случае матрица S не треугольная.
Алгоритм 2 нахождения ранних сроков окончания выполнения работ.
- Полагаем первоначально ?11 = ?12 = ... = ?1m
= 0.
- Производя циклический обзор строк матрицы S, находим очередную из необработанных строк.
Если все строки обработаны, выполнение алгоритма заканчивается. - Пусть j — номер найденной необработанной строки. Если j-я строка не содержит единичных элементов, полагаем ?1j = tj. Переходим к выполнению шага 6.
- Если j-я строка содержит единичные элементы, выбираем элементы множества {?11 , ... , ?1m}, соответствующие номерам единичных элементов j-й строки.
Если все выбранные таким образом элементы, образующие множество {?1j(?)}, ? = 1, ... , kj, отличны от нуля, полагаем ?1j = max ?1 j? + tj.
Если хотя бы один из выбранных элементов нулевой (соответствующий ранний срок ещё не найден), выполняем шаг 2.
Обработанную j-ю строку метим, чтобы исключить её повторную обработку. Переходим к выполнению шага 2.
Примечание. Если граф G не содержит контуров, зацикливание при этом невозможно.
Конец алгоритма.
Если матрица S треугольная, то никогда не складываются условия для многократного циклического обзора строк. Тогда ранние сроки окончания выполнения работ находятся за один последовательный просмотр строк матрицы S.
Очевидно, что Tкр = max {?11 , ... , ?1m}.
По матрице S* ( S — треугольная) на рис. 7.5 (граф G — на рис. 7.1) находим
?11 = t1 = 2, ?12 = t2 = 3, ?13 = ?11 + t3
=3, ?14
= ?11 + t4 = 4, ?15 = max {?11, ?12 + t5= 7, ?16 = max {?11, ?14} + t6 = 8, ?17 = max {?12,?14 } + t7 = 6, ?18 = max {?13, ?15, ?16, ?17} + t8 = 9; Tкр = 9.
Чтобы рассмотреть пример с нетреугольной матрицей следования, выберем граф G без контуров с "неправильно" пронумерованными вершинами (рис. 7.10).
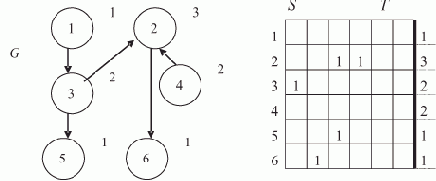
Рис. 7.10. Информационный граф с не треугольной матрицей следования
После обработки первой строки ?11 = 1. Попытка обработать вторую строку неудачна, т.к. ?13 и ?14 ещё не найдены. После обработки третьей строки ?13 = ?11 + t3 = 3. Обработка четвёртой строки даёт ?14 = 2. После обработки пятой строки ?15 = ?13 + t5 = 4. Попытка обработки шестой строки неудачна, т.к. не найдено значение ?12. Приступаем к следующему циклу обзора необработанных строк S. Обрабатываем вторую строку: ?12 = max {?13, ?14} + t2 = 6.
После обработки шестой строки ?16 = ?12 + t6 = 7. Tкр = 7.
Для удобства представления наряду с другими способами будем пользоваться наглядными диаграммами выполнения работ при заданных значениях времени начала или окончания их выполнения. Работы обозначаются прямоугольниками с постоянной высотой и длиной, равной времени выполнения. Стрелки, связывающие прямоугольники-работы, соответствуют дугам в графе G. На рис. 7.11 представлена диаграмма выполнения работ, отраженных графом G на рис. 7.1 и расширенной матрицей следования на рис. 7.5 — при ранних сроках выполнения работ.
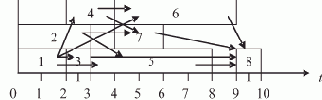
Рис. 7.11. Временная диаграмма выполнения работ при ранних сроках окончания
Алгоритм 3 нахождения поздних сроков окончания выполнения работ при заданном значенииТ.
- Полагаем первоначально ?21(T) = ... = ?2m(T) = 0.
- Производя циклический обзор справа налево столбцов матрицы S, находим очередной из не обработанных ещё столбцов. Если все столбцы обработаны, выполнение алгоритма заканчивается.
- Пусть j — номер найденного необработанного столбца. Если j-й столбец не содержит единичных элементов, полагаем ?2j(T) = T. Переходим к выполнению шага 6.
- Если j-й столбец содержит единичные элементы, выбираем элементы множества { ?21(T) , ... ,?2m(T) }, соответствующие номерам единичных элементов j-го столбца.
Если все выбранные таким образом элементы {?2j?}(T)}{?21(T), ... , ?2m(T)}, ? = 1 , ... , kj, отличны от нуля, полагаем
?2j (T) = min {?2j? (T) - tj? }.
В противном случае выполняем шаг 2.
- Обработанный j-й столбец метим с целью исключения его повторной обработки. Переходим к выполнению шага 2.
Конец алгоритма.
Если матрица S — треугольная, то поздние сроки окончания выполнения работ находятся за один просмотр столбцов.
Для матрицы S* (матрица S — треугольная) на рис. 7.5 и для T = 10 за один просмотр находим
?28(10) = 10, ?27(10) = ?28(10) - t8 = 9, ?26(10) = ?28(10)- t8 = 9, ?25(10) = ?28(10) - t8 = 9 , ?24 = min {?26(10), - t6, ?27(10) - t7} = 5, ?23(10) = ?28(10) - t8 = 9, ?22(10) = min {?25(10) - t5, ?27(10) - t7 } = 5, ?21(10) = min {?23(10) - t3, ?24(10) - t4, ?25(10) - t5, ?26(10) - t6} = 3.
Для нетреугольной матрицы S на рис. 7.10 при T = 10 находим ?26(10) = ?25(10) = 10. Обработка четвёртого столбца откладывается, т.к. не найдено значение ?22(10). По этой же причине не обрабатывается третий столбец. После обработки второго столбца находим ?22(10) = ?26(10) - t6 = 9.
Обработка первого столбца невозможна, т.к. ещё не найдено значение ?23(10). Продолжаем циклический обзор столбцов. После обработки четвёертого столбца получаем ?24(10) = ?22(10) - t2 = 6. Обработка третьего столбца даёт ?23(10) = min {?22(10) - t2, ?25(10) - t5} = 6. После обработки первого столбца находим ?21(10) = ?23(10) - t3 = 4.
Диаграммы выполнения работ при поздних сроках окончания, по графам на рис. 7.1 и 7.10, при T = 10 представлены на рис. 7.12 — (а) и (б), соответственно. (Стрелки, соответствующие дугам в графах, опущены в связи с их избыточностью.)
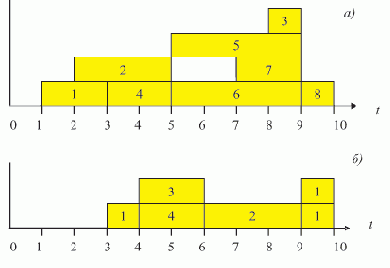
Рис. 7.12. Диаграммы выполнения работ при поздних сроках окончания: а — для графа на рис. 7.1,б — для графа на рис. 7.10
Пусть ?j — произвольное значение момента окончания выполнения j-й работы, j =1 , ... , m,
?1j



Меняя значения {?j}, j = 1 , ... ,m, но соблюдая при этом порядок следования работ, мы получим множество допустимых расписаний выполнения работ.
Нашей конечной целью является выбор таких расписаний, которые позволяют решить задачи 1 и 2.
Определение 7. Функцию

назовём плотностью загрузки, найденной для значений ?1 , ... , ?m.
Для заданных ?1 , ... , ?m значение функции F в каждый момент времени t совпадает с числом одновременно (параллельно) выполняющихся в этот момент работ.
Например, по диаграмме на 7.11, т.е. для ?1 = ?11, ?2 = ?12, ... , ?8 = ?18, функция F(2, 3, 3, 4, 7, 8, 6, 9, t) имеет вид, представленный на рис. 7.13а. Для допустимого расписания, определяемого набором значений ?1 = 2, ?2 = 4, ?3 = 3, ?4 = 4, ?5 = 8, ?6 = 9, ?7 = 7, ?8 = 10, функция F(2, 4, 3, 4, 8, 9, 7, 10, t) имеет вид, представленный на рис. 7.13б.
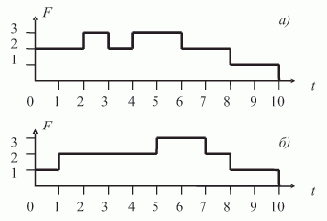
Рис. 7.13. Графики функции: а — для ранних сроков окончания работ,,б — для некоторого допустимого расписания
Для графического представления функции F удобно пользоваться временной диаграммой, которая для второго случая, например, имеет вид, представленный на рисунке 7.14..
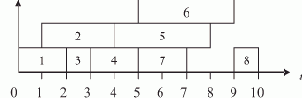
Рис. 7.14. Временная диаграмма функции F
Пусть данный граф G, в котором учтены транзитивные связи, образует l полных множеств взаимно независимых работ (ПМВНР). (Каждая пара таких множеств может иметь непустое пересечение.) Обозначим ri, i = 1 , ... , l, число работ, образующих i-е полное множество и найдём
R = max {r1 , ... , rl}.
Тогда

т.к. возможно и такое распределение выполняемых работ во времени, задаваемое набором ?1 , ... , ?m, (т.е. допустимое расписание), когда на каком-то отрезке времени выполняются все работы, составляющие ПМВНР с числом R работ.
Например, для графа на рис. 7.1 мы нашли ПМВНР {3,5,6,7}, включающее четыре работы. Тогда существует допустимое расписание, например, ?1 = 2, ?2 = 3, ?3 = 5, ?4 = 4, ?5 = 8, ?6 = 8, ?7 = 6, ?8 = 9 такое, при котором максимальное значение плотности загрузки F равно четырём (рис. 7.15).
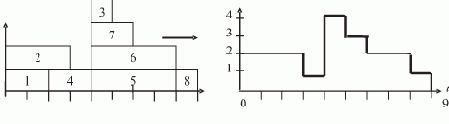
Рис. 7.15. Максимальное значение плотности загрузки
Таким образом, справедливо утверждение
Лемма. Минимальное число n процессоров одинаковой специализации и производительности (т.е. в однородной ВС), способных выполнить данный алгоритм за время T

Определение 8. Функцию

назовём загрузкой отрезка [?1, ?2]

Функция Ф определяет объём работ (суммарное время их выполнения) на фиксированном отрезке их выполнения при заданном допустимом расписании.
Так, для отрезка времени [0, 4]

Ф = 10 и т.д.
Определение 9. Функцию

назовём минимальной загрузкой отрезка [?1, ?2]

Функция определяет минимально возможный объём работ, который при данном T и при различных допустимых значениях (расписаниях) ?1 , ... , ?m
должен быть выполнен на отрезке времени [?1, ?2]

мы не выбрали, объём работ, выполняемых на отрезке времени [?1, ?2], не может быть меньше значения

Теорема 1. Для того чтобы T было наименьшим временем выполнения данного алгоритма однородной вычислительной системой, состоящей из n процессоров, либо чтобы n процессоров было достаточно для выполнения данного алгоритма за время T, необходимо, чтобы для данного отрезка времени [?1, ?2]

 | (7.1) |
Доказательство. Нетрудно видеть, что если при данном наборе ?1 , ... , ?m — сроках окончания выполнения работ, в том числе и при таком наборе, при котором обеспечивается минимальное или заданное T = max {?1
, ... , ?m}, для реализации алгоритма достаточно n процессоров, то

Отсюда, для любого отрезка времени [?1, ?2]


что и требовалось доказать.
Необходимость, но не достаточность условия (7.1) покажем на примере. Пусть алгоритму соответствует граф G на рис. 7.16а. Пусть T=3, и одна из возможных диаграмм выполнения алгоритма — на рис. 7.16б.
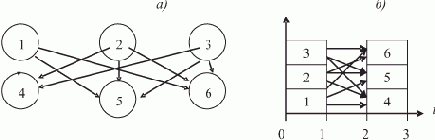
Рис. 7.16. Пример: минимальная плотность загрузки не соответствует действительной: а — информационный граф, б — временная диаграмма загрузки
Оценим на основе (7.1) число n процессоров, достаточное для выполнения алгоритма в указанное время. Из (7.1) имеем общее соотношение
 | (7.2) |

 | (7.3) |







Находим минимальное n = 2, удовлетворяющие (7.3). Однако из рисунка видно, что не существует плана выполнения работ на двух процессорах за время T=3. Минимально достаточное число процессоров здесь n = 3.
Функция

Предварительно определим функцию

Тогда значение ?(?1j - ?1) характеризует условный объём части работы j на отрезке времени [?1, ?2] при условии ?1j
- tj

Значение ? (?2 - ?2j(T) + tj) характеризует аналогичный объём работы j при максимальном смещении времени выполнения работы j вправо. Это соответствует, например, ситуации, изображённой на рис. 7.17б.
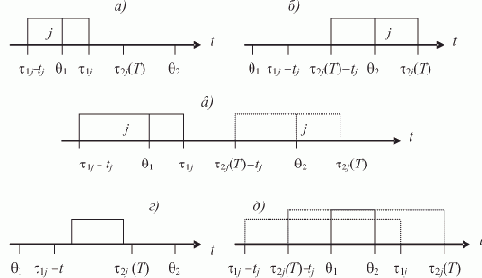
Рис. 7.17. Нахождение минимальной плотности загрузки отрезка: все различные случаи соотношения времени выполнения работ и сроков
Если для работы j оба указанных выше значения функции ? отличны от нуля, но не превышают значение tj и ?2 - ?1, то максимально разгрузить отрезок [?1, ?2] от работы j можно смещением времени его выполнения в сторону, обеспечивающую меньшее из двух указанных выше значений ? (рис. 7.17в).
Существуют два случая, когда работа j не может быть хотя бы частично смещена с отрезка [?1, ?2] :
а) ?1


?2, в этом случае очевидно, что tj

(рис. 7.17г), и объём работы j, выполняемой на отрезке, совпадает с объёмом tj всей этой работы;
б) ?1j



(рис. 7.17д), и объём части работы j, выполняемой на отрезке [?1, ?2] совпадает со значением ?2 - ?1.
Приведённый ниже алгоритм объединяет все возможные указанные выше случаи.
Алгоритм 4 нахождения значения функции

1. Предполагаем, что для каждой работы j = 1, ... , m, известны значения tj, ?1j, ?2j(T). Полагаем равным нулю значение переменной

2. Организуем последовательный анализ работ j = 1, ... , m.
3. Для каждой работы j полагаем


После перебора всех работ


Конец алгоритма.
Выше было получено соотношение (7.2) , которое можно использовать для нижней оценки количества n процессоров, необходимых для выполнения данного алгоритма за время, не превышающее T.
Приведём аналогичное соотношение для нижней оценки минимального времени Т.
Теорема 2. Пусть заданный алгоритм выполняется на ВС, состоящей из n процессоров, и T* — текущее значение оценки снизу времени выполнения алгоритма. Пусть на отрезке времени [?1, ?2]


Тогда минимальное время T выполнения алгоритма удовлетворяет соотношению
 | (7.4) |
Теоремы 1 и 2 на основе анализа такой локальной характеристики параллельного алгоритма, как значение функции

- числа n процессоров при заданном ограничении на длительность T процесса;
- минимального времени T, необходимого для реализации данного алгоритма при заданном числе n процессоров.
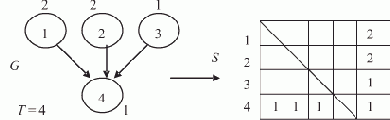
Рис. 7.18. К примеру нахождения нижней оценки числа исполнителей
