Решение задачи 1 распараллеливания для однородных ВС

Формулировка задачи: Для данного алгоритма, которому соответствует информационный граф G, и для времени T, отведённого для его выполнения, найти наименьшее число n процессоров, составляющих однородную ВС, и план выполнения работ на них.

Метод точного решения задачи (метод "ветвей и границ") основан на следующей основной теореме.

Теорема. Для того чтобы значение n являлось наименьшим числом процессоров однородной ВС, которая выполняет алгоритм, представленный информационным графом G = (X, P, Г ), за время, не превышающее заданное значение T, необходимо и достаточно, чтобы n было наименьшим числом, для которого можно построить граф G' = (X, P, Г'), объединив вершины, соответствующие работам каждого ПМВНР, который содержит r > n работ r - n ориентированными дугами в n путей не содержащих общих вершин. При этом длина критического пути в графе G' не должна превышать значение T.

Алгоритм 7 решения задачи 1 — нахождения графа-решения G'

Для графа G и времени T находим значения ранних {?1j} и поздних {?j(T)}, j = 1 , ... , m, сроков окончания выполнения работ. (Если задача поставлена корректно, то
Находим оценку минимального числа n процессоров, которое необходимо для выполнения заданного алгоритма за время, не превышающее T.
Пусть ? — номер шага решения задачи. Полагаем ? = 1.
Находим наименьшее значение t? такое, что

F(?11, ?12 , ... , ?1m, t? ) = r? > n.

Если такого t? нет, то n — решение задачи.
Выделяем множество работ A? = {
j?}, ? =1 , ... , r?, для которых

?1j? - tj?
t? < ?1?,

т.е. тех работ, которые "порождают" данное значение F. Множество A является подмножеством некоторого ПМВНР.
Предположим, что мы можем упорядочивать комбинации дополнительных связей внутри множества A?. Введём очередную комбинацию r - n связей, как указано в теореме — так, чтобы длина критического пути в изменившемся при этом графе G не превысила T.
Если такая комбинация найдена, выполняем операцию ? := ? + 1, уточняем значения {?1j} и {?2j(T)} с учётом введённых связей, переходим к выполнению 4.
Если такой комбинации связей не существует, либо все они уже испытаны, выполняем операцию ? := ? - 1.
Если ? = 0, т.е.
на первом же шаге сглаживание загрузки процессоров не приводит к подтверждению того, что n — решение, выполняем операцию n := n + 1 и переходим к выполнению 3. Если ?
0, восстанавливаем значения {?1j} и {?2j(T)} , найденные на данном шаге, и переходим к выполнению 6.

Конец алгоритма.
Таким образом, суть алгоритма в том, что, реализуя общий подход, который называется метод "ветвей и границ", мы, выбрав начальное расписание, где все работы занимают на оси времени крайнее левое положение, продвигаемся шаг за шагом и находим точки на оси времени, в которых функция плотности загрузки превышает первоначально испытываемое n. Пытаемся сгладить значение этой функции, введя дополнительные связи между работами, допускаемые ограничением T. В случае неудачи вернёмся на шаг назад и попытаемся ввести другую комбинацию связей. При переборе всех комбинаций связей на первом шаге, не приведших к успеху, увеличим предполагаемое число процессоров и начнём процесс сглаживания функции плотности загрузки сначала.
Примечания

Как упорядочить вводимые комбинации связей?
Пусть A? — множество взаимно независимых работ, между которыми нужно ввести r - n связей по условию теоремы, т.е. построить некоторый граф, связывающий вершины A?. Построим матрицу следования L?, соответствующую этому графу. Первоначально эта матрица — нулевая. Вводим r? - n единиц так, чтобы:
- граф, соответствующий получаемой при этом матрице, не содержал контуров (отсюда, в частности, следует, что диагональные элементы всегда должны быть нулевыми);
- в каждой строке и в каждом столбце матрицы не должно содержаться больше одной единицы (следует из Теоремы о возможных путях, не содержащих общих работ).
Перемещая последнюю единицу сначала по строке, затем по столбцам, затем перейдя к предпоследней единице и т.д., осуществляем перебор всех возможных комбинаций связей между работами множества A?.
Можно рекомендовать следующий способ сокращения перебора: введение дополнительных связей в пункте 6 алгоритма производить не только по критерию допустимого увеличения длины критического пути, но и по значениям функции минимальной загрузки отрезка.

А именно, вводя очередную комбинацию связей на ?-м шаге сглаживания функции плотности загрузки, не приводящую к увеличению длины критического пути сверх заданного T, необходимо вновь пересчитать значение функции
с учётом новых связей на всех отрезках [?1, ?2]
[t?, T] . Если для испытываемого значения n на этих отрезках выполняется соотношение (7.2), данная комбинация связей может быть признана удачной. Таким образом, выполнение соотношения (7.2) в совокупности с допустимым увеличением длины критического пути определяет "границы" при ветвлении.

(Напомним, что метод "ветвей и границ", как метод перебора, обладает экспоненциальной сложностью, является NP-трудным. Поэтому сокращение перебора — очень важная задача.)
Пример.
Найдём минимальное число n процессоров, необходимое для выполнения алгоритма, который представлен графом G на рисунке 7.21а, за время T = 7.

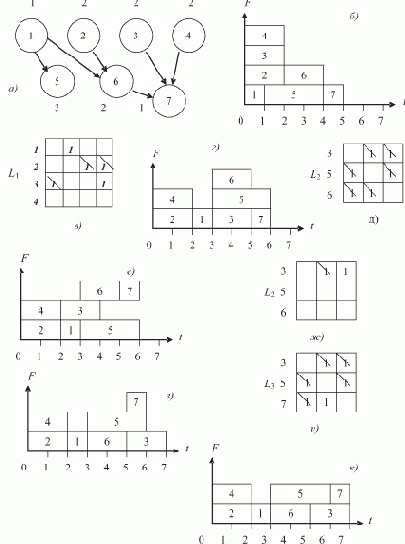
Рис. 7.21. Последовательные действия при точном решении задачи 1
По алгоритму 4 найдёем нижнюю оценку n = 2, исследовав 28 значений

(7)(?1,?2) для всех [?1, ?2]

[0, 7] . При этом ?11 = 1, ?12 = ?13
= ?14 = 2, ?15 = ?16 = 4, ?17 = 5, ?21(7) = ?22(7) = 4, ?23 (7) = ?24(7) = ?26 (7) = 6, ?25(7) = ?27 = 7. Мы не собираемся впредь иллюстрировать нахождение функции минимальной загрузки, поэтому не будем приводить динамически уточняемые значения поздних сроков окончания выполнения работ.
F(?11 , ... , ?17) = 4 > 2, т.е. t1 = 0. В формировании этого значения участвуют работы 1, 2, 3, 4. Составим квадратную матрицу L1 (рис. 7.21в) с первоначально нулевыми элементами. Постараемся последовательно ввести в неё два единичных элемента. Первая возможная комбинация двух таких элементов соответствует связям 3

1. Длина критического пути в графе G, дополненном дугами в соответствии с этими связями, превышает 7. Пробуем заменить вторую связь следующей возможной. Новая испытываемая комбинация связей 4

1 также приводит к недопустимому увеличению длины критического пути. Единичные элементы, соответствующие отвергнутым связям, на рисунке зачёркнуты.

Вновь меняем вторую связь, полагая равным единице первый элемент третьей строки матрицы L1. Новая комбинация связей 2

3 не приводит к недопустимому увеличению длины критического пути в графе G. По графу, учитывающему введённые связи, находим ранние и поздние сроки окончания выполнения работ. На рис. 7.21г, приведена диаграмма выполнения алгоритма при ранних сроках {?11 = 3, ?12 = ?14 = 2}, ?13 = ?16 = 5, ?15 = ?17 = 6 окончания выполнения работ. Связи между работами не указаны.
Найдём t2 = 3 такое, что F(3, 2, 5, 2, 6, 5, 6, 3) = 3 > 2. Данное значение функции плотности загрузки определяется выполнением работ 3, 5, 6. Составляем матрицу L2 (рис. 7.21д) и стараемся ввести в ней единственный единичный элемент. Однако перебор всех возможных способов введения такого элемента приводит к длине критического пути в образующемся графе, превышающей 7. Возвращаемся на шаг назад к анализу матрицы L1 и пробуем ввести другую допустимую комбинацию связей. Такой комбинацией является 2

1, 4

3. На рис. 7.21е
представлена диаграмма выполнения алгоритма при уточнённых ранних сроках окончания выполнения работ ?11 = 3, ?12 = ?14 = 2 ?13 = 4, ?15 = ?17 = 6, ?16 = 5
Вновь находим значение t2 = 3 такое, что F(3, 2, 4, 2, 6, 5, 6, 3) = 3 > 2. (Совпадение значений t2 и выделенных работ с ранее исследованными является скорее случайным.) Вновь формируем матрицу L2 (индекс указывает номер шага, новая матрица L2 в общем случае ничем не схожа с аналогичной ранее рассмотренной матрицей), и находим первую из допустимых связей — связь 6

3 (рис. 7.21ж).
Вновь (рис. 7.21з) находим значение t3 = 5, где плотность загрузки превышает значение 2. Составляем матрицу L3 (рис. 7.21и). Находим в ней единственную единицу, соответствующую допустимой связи 5

7. На рис. 7.21к представлена диаграмма выполнения алгоритма, удовлетворяющая решению задачи.
Собственно расписание определяется найденными на последнем шаге значениями {?1j} .

Содержание раздела