Исходные построения
Исследование потоков в сети — важная, всегда актуальная задача исследования операций. Она лежит в основе моделирования при проектировании как транспортных сетей, так и сетей водоснабжения и канализации. Известен ряд классических моделей (приводимых, например, в [15]) в этой области. Важнейшую роль играют модели, позволяющие определить "узкие" мести сети. Они определяют ее максимальную пропускную способность между выделенными пунктами, или, иначе говоря, ее минимальное сечение. Это задача дискретного программирования, широко использующая перебор и относящаяся к задачам высокой сложности.
При аналитическом моделировании сети используется известный [15] алгоритм Форда-Фалкерсона.
Теория параллельного программирования способна предложить более простой алгоритм перебора. Его достоинством является параллелизм, который позволяет эффективно использовать многопроцессорные ВС и вычислительные комплексы на основе рабочих станций локальной сети. Возможен наиболее простой способ распараллеливания на основе применения SPMD-технологии.
Пусть задана сеть (рис. 5.1). Дуги ее назовем каналами. Каналы пронумерованы. Направление потоков показано стрелками. Вершины — точки сопряжения каналов, вершина A — исток, вершина B — сток. Каждая дуга i сопровождается информацией об интересующих нас характеристиках потока, например, о пропускной способности di канала. В этом случае правомерен вопрос о максимальной пропускной способности сети, обусловленной минимальным сечением.
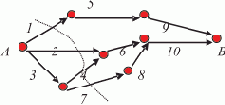
Рис. 5.1. Сеть для оценки пропускной способности
В терминах теории параллельного программирования (лекция 7) каждое сечение сети (например, сечение, пересекающее каналы 1, 2, 4, 7) является полным множеством взаимно независимых работ — каналов (ПМВНК). Перебрав все такие множества и рассчитав для каждого суммарную пропускную способность, мы можем найти минимальное значение. Оно характеризует минимальное сечение, а следовательно, максимальный возможный поток в сети.
В [3] приводится алгоритм перебора всех полных множеств взаимно независимых работ.
Усовершенствуем его, получая такие множества, упорядоченные по номерам каналов, и исключая повторное нахождение одних и тех же полных множеств. (В лекции 7 изложенные ниже преобразования будут рассмотрены глубже.)
Построим треугольную матрицу следования S, отражающую граф сети (рис. 5.2а). Сложив каждую последующую строку с теми предыдущими, которые соответствуют единичным элементам этой строки, получим матрицу следования S с транзитивными связями (рис. 5.2б). Транспонируем матрицу S и объединим с ее начальным видом (рис. 5.2в). Иначе, отобразим S симметрично относительно главной диагонали. Получим матрицу S, отображающую как порядок следования, так и порядок предшествования каналов.
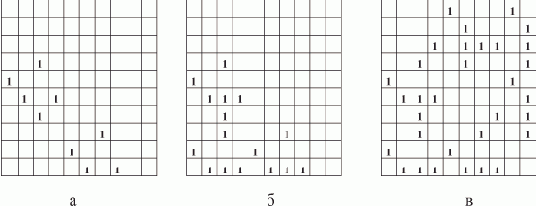
Рис. 5.2. Полная матрица следования каналов:а — начальный вид, б — дополнение транзитивными связями, в — конечный вид
Теперь матрица S полностью отражает взаимную независимость каналов. Например, если сложить логически строки 1, 2, 3, то получим строку, содержащую нули только в позициях 1, 2, 3. Тем самым мы получим ПМВНК {1, 2, 3}. Множество полное, т.к. дополнительное сложение с любой другой строкой изменит состав нулей.
Таким образом, наша задача заключается в том, чтобы испытать все варианты сложения групп строк так, чтобы нули в строке-результате оказывались в тех и только в тех позициях, которые соответствуют строкам- слагаемым. Тогда эти строки определят очередное ПМВНК. Упорядочение по номерам строк поможет нам избежать повторного получения ПМВНК с другим порядком следования номеров каналов.
